About Authors:
LILESH KHALANE*, ATUL ALKUNTE, ARUNADEVI BIRAJDAR
Adarsh Shikshan Prasarak Mandal’s, K. T. Patil college of Pharmacy,
Siddhartha Nagar, Barshi Road,
Osmanabad – 413501.
*lileshkhalane@gmail.com
ABSTRACT
As a very few drugs are coming out of research and development and already existing drugs are suffering the problem of resistance due to their irrational use. Hence, change in the operation is a suitable and optimized way to make the some drug more effective by slight alternation in the drug delivery. Presently pharmaceutical industries are focusing on development of sustained release formulations due to its inherent boons. Sustained release dosage forms are designed to release a drug at a predetermined rate by maintaining a constant drug level for a specific period of time with minimum side effects. The basic rationale of sustained release drug delivery system optimizes the biopharmaceutical, pharmacokinetic and pharmacodynamics properties of a drug in such a way that its utility is maximized, side-effects are reduced and cure of the disease is achieved. There are several advantages of sustained release drug delivery over conventional dosage forms like improved patient compliance due to less frequent drug administration, reduction of fluctuation in steady-state drug levels, maximum utilization of the drug, increased safety margin of potent drug, reduction in healthcare costs through improved therapy and shorter treatment period. The basic goal of sustained release is provide promising way to decrease the side effect of drug by preventing the fluctuation of the therapeutic concentration of the drug in the body and increase patient compliance by reducing frequency of dose. This article contains the basic information regarding sustained-release formulation and also the different types of the same.
Reference Id: PHARMATUTOR-ART-1433
INTRODUCTION
A drug delivery system (DDS) is defined as a formulation or a device that enables the introduction of a therapeutic substance in the body and improves its efficacy and safety by controlling the rate, time, and place of release of drugs in the body. This process includes the administration of the therapeutic product, the release of the active ingredients by the product, and the subsequent transport of the active ingredients across the biological membranes to the site of action. The term therapeutic substance also applies to an agent such as gene therapy that will induce in vivo production of the active therapeutic agent. Drug delivery system is an interface between the patient and the drug. It may be a formulation of the drug to administer it for a therapeutic purpose or a device used to deliver the drug. This distinction between the drug and the device is important, as it is the criterion for regulatory control of the delivery system by the drug or medicine control agency. If a device is introduced into the human body for purposes other than drug administration, such as therapeutic effect by a physical modality or a drug may be incorporated into the device for preventing complications resulting from the device, it is regulated strictly as a device. There is a wide spectrum between drugs and devices, and the allocation to one or the other category is decided on a case by case basis. Sustained release (SR) preparations are not new but several new modifications are being introduced. They are also referred to as “long acting” or “delayed release” when compared to “rapid” or “conventional” release preparations. The term sometimes overlaps with “controlled release,” which implies more sophisticated control of release and not just confined to the time dimension.
The following are the rationale of developing SR1, 2, 3
1) To extend the duration of action of the drug
2) To reduce the frequency of dosing
3) To minimize the fluctuations in plasma level
4) Improved drug utilization
5) Less adverse effects
Advantages of sustained release dosage forms1, 2, 3
1) The frequency of drug administration is reduced.
2) Patient compliance can be improved.
3) Drug administration can be made more convenient as well.
4) The blood level oscillation characteristic of multiple dosing of conventional dosage forms is reduced.
5) Better control of drug absorption can be attained, since the high blood level peaks that may be observed after administration of a dose of a high availability drug can be reduced.
6) The characteristic blood level variations due to multiple dosing of conventional dosage forms can be reduced.
7) The total amount of drug administered can be reduced, thus:
· Maximizing availability with minimum dose;
· Minimize or eliminate local side effects;
· Minimize or eliminate systemic side effects;
· Minimize drug accumulation with chronic dosing.
8) Safety margins of high potency drugs can be increased and the incidence of both local and systemic adverse side effects can be reduced in sensitive patients.
9) Improve efficiency in treatment.
· Cure or control condition more promptly
· Improve control of condition
· Improve bioavailability of some drugs
· Make use of special effects; e.g. sustain release aspirin for morning relief of arthritis by dosing before bed-time.
10) Economy.
Disadvantages of sustained release dosage forms1, 2, 3
1) Probability of dose dumping.
2) Reduced potential for dose adjustment.
3) Cost of single unit higher than conventional dosage forms.
4) Increase potential for first pass metabolism.
5) Requirement for additional patient education for proper medication.
6) Decreased systemic availability in comparison to immediate release conventional dosage forms.
7) Poor invitro and invivo correlations.
TERMINOLOGY4, 5
The general consensus is that controlled release denotes systems, which can provide some control, whether this is of a temporal or spatial nature, or both, of drug release in the body. In other words, the systems attempts to control drug concentration in the target tissue or cells. Thus, prolonged release or sustained release systems, which only prolonged therapeutic blood or tissue levels of the drug for an extended period of time, cannot be considered as controlled release systems by this definition. They are distinguished from rate-controlled drug delivery systems, which are able to specify the release rate and duration in vivo precisely, on the basis of simple invitro tests. Drug targeting; on the other hand, can be considered as a form of controlled release in that exercises spatial control of drug release within the body. In general, controlled delivery attempts to:
· Sustain drug action at a predetermined rate by maintaining a relatively constant, effective drug level in the body with concomitant minimization of undesirable side effects associated with a saw tooth kinetic pattern.
· Localize drug action by spatial placement of a controlled release system (Usually rate-controlled) adjacent to or in the diseased tissue or organ.
· Target drug action by using carriers or chemical derivatization to deliver drug to a particular “target” cell type.
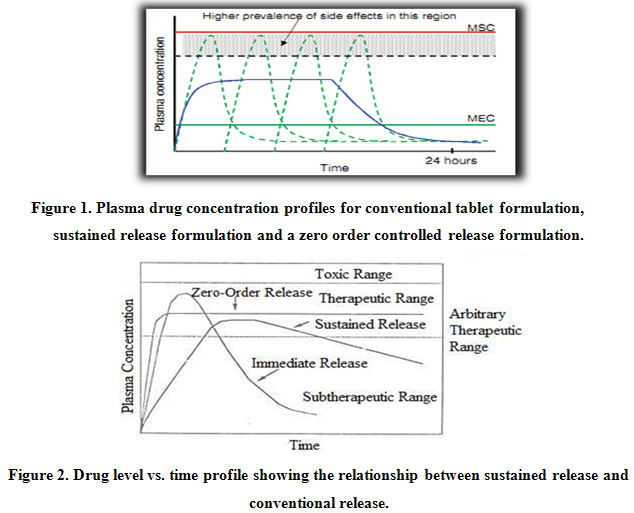
In practice, very few of the applied systems embrace all of these actions. In most cases, the release systems create constant concentration of drug within the body over an extended period of time. The assumption is that there is steady state drug levels in plasma and in target tissue or cells are correlated. Ideally, it is desirable to place the drug at the target, be it a tissue, a population of cells or receptors, leaving the rest of body drug free. Obviously this would be quite difficult, especially if the target is sheltered from systemic circulation by various barriers. For example, drug targeting to the brain via systemic administration is severely limited by selectivity of the blood-brain barrier.Figure 1 and 2 shows comparative blood level profiles obtained from administration of conventional, controlled, and sustained release dosage forms. The conventional tablet or capsule provides only a single and transient burst of drug. A pharmacological effect is seen as long as the amount of drug within the therapeutic range. Problems occur when the peak concentration is above or below this range, especially for drugs with narrow therapeutic windows. Indeed, prolonged release dosage forms reduce fluctuations in plasma drug levels by slowing down the absorption rate due to slower drug release rate.
The term “sustained release” is known to have existed in the medical and pharmaceutical literature for many decades. It has been constantly used to describe a pharmaceutical dosage form formulated to retard the release of therapeutic agent such that its appearance in the systemic circulation is delayed and/or prolonged and its plasma profile is sustained in duration.
The term “controlled release”, on the other hand, has a meaning that goes beyond the scope of sustained drug action. It also implies a predictability and reproducibility in the drug release kinetics, which means that the release of drug from controlled – release drug delivery system proceeds at a rate profile that is not predictable kinetically, but also reproducible from one unit to another.
THEORETICAL OVERVIEW1, 5, 6, 7
The basic goal of therapy is to achieve a steady - state blood or tissue level that is therapeutically effective and nontoxic for extended period of time. Modified-release delivery systems may be divided conveniently into four categories:
1) Delayed release.
2) Sustain release.
3) Site-specific targeting.
4) Receptor targeting.
Delayed release systems are those that use repetitive, intermittent dosing of a drug from one or more immediate-release units incorporated into a single dose form. Example delayed release system include repeat action tablets, capsules and enteric coated tablet where timed release is achieved by barrier coating.
Sustain release system includes any drug delivery systems that achieves slow release of drug over an extended period of time. If the systems can provide some control, whether this is of temporal or spatial nature, or both, of drug release in the body, or in other words, the system is successful at maintaining constant drug levels in the target tissue or cells, it is considered a controlled-release system.
Site-specific targeting refers to targeting of drug directly to a certain biological locations. In the case of site-specific release, the target is adjacent to or in the diseased organ or tissue.
Receptor targeting refer to the target is particular receptor for a drug within an organ or tissue. Both of these systems satisfy the spatial aspects of drug delivery and are also considered to be controlled-drug delivery systems.
BIOLOGICAL FACTORS INFLUENCING ORAL SUSTAINED-RELEASE DOSAGE FORM DESIGN3, 7
Biological Half-Life
The usual goal of an oral sustained-release product is to maintain therapeutic blood levels over an extended period. The elimination rate is quantitatively described by the half-life. Each drug has its own characteristic elimination rate, which is the sum of all elimination process, including metabolism, urinary excretion, and all other processes that permanently remove drug from the bloodstream.
Therapeutic compound with short half-lives are excellent candidates for sustained release preparations, since this can reduce dosing frequency. However, this is limited, in that drug with very short half-lives may require excessively large amounts of drug in each dosage unit to maintain sustained effect, forcing the dosage form itself to become limitingly large. In general, drugs with half-lives shorter than 2 hours are poor candidates for sustained-release preparations. Compounds with long half-lives, more than 8 hours, are also generally not used in sustaining forms, since there effect is already sustained.
Absorption
The characteristics of absorption of a drug can greatly affect its suitability as a sustained-release product. Since the purpose of forming a sustained-release product is to place control on the delivery system, it is necessary that the rate of release much slower than the rate of absorption. If we assume that the transits time of most drugs and devices in the absorptive areas of the GI tract is about 8-12 hours, the maximum half-life for absorption should be approximately 3-4 hours; otherwise, the device will pass out of the potential absorptive regions before drug release is complete. This corresponds to a minimum apparent absorption rate constant of 0.17-0.23 hours-1 to give 80-95% over this time period. The absorption rate constant is an apparent rate constant, and should, in actuality, be the release rate constant of the drug from the dosage form. Compounds that demonstrate true lower absorption rate constants will probably be poor candidates for sustaining system.
Distribution
The distribution of drugs into tissue can be an important factor in the overall drug elimination kinetics since it not only lowers the concentration of circulating drug but it also can be rate limiting in its equilibration with blood and extracellular fluid. One aspect of this distribution is binding of drug to tissue and proteins in blood. The apparent volume of distribution of a drug is frequently used to describe the magnitude of distribution, including binding, within the body. For design of sustained/controlled release products one would like to have as much information on drug disposition as possible but, in reality, decisions are usually based on only a few pharmacokinetic parameter, one of which is the apparent volume of distribution.
Metabolism
Drugs that are significantly metabolized before absorption, either in the lumen or tissue of the intestine, can show decreased bioavailability from slower-releasing dosage forms. Most intestinal wall enzyme systems are saturable. As the drug is released at a slower rate to these regions, less total drug is presented to the enzymatic process during specific period, allowing more complete conversion of the drug to its metabolites. Formulation of these enzymatically susceptible compounds as prodrugs is another viable solution.
PHYSICOCHEMICAL FACTORS INFLUENCING ORAL SUSTAINED-RELEASE DOSAGE FORM DESIGN3, 7
Dose Size
For orally administered systems, there is an upper limit to the bulk size of the dose to be administered. In general, a single dose of 0.5-1.0 gm is considered maximal for a conventional dosage form. This also holds for sustained-release dosage forms. Those compounds that require large dosing size can sometimes be given in multiple amounts or formulated into liquid system. Another consideration is the margin of safety involved in administration of large amounts of a drug with narrow therapeutic range.
Aqueous Solubility
Compounds with very low solubility (less than 0.01mg/ml) are inherently sustained, since there release over the time course of a dosage form in the GI tract will be limited by dissolution of the drug. The lower limit for the solubility of a drug to be formulated in a sustained-release system has been reported to be 0.1mg/ml, so it is obvious that the solubility of the compound will limit the choice of mechanism to be employed in sustained delivery system. Diffusional systems will be poor choices for slightly soluble drugs, since the driving force for diffusion, which is the drug’s concentration in solution, will be low.
Partition Coefficient
When a drug is administered to the GI tract it must cross a variety of biological membranes to produce a therapeutic effect in another area of the body. It is common to consider that these membranes are lipidic; therefore, the partition coefficient of oil-soluble drugs becomes important in determining the effectiveness of membrane barrier penetration. Partition coefficient is generally defined as the ratio of the fraction of drug in an oil phase to that of an adjacent aqueous phase. Accordingly, compounds with a relatively high partition coefficient are predominantly lipid-soluble and, consequently, have very low aqueous solubility.
Stability
Orally administered drugs can be subject to both acid-base hydrolysis and enzymatic degradation. Degradation will proceed at a reduced rate for drugs in the solid state; therefore, this is the preferred composition of delivery for problem cases. For drugs that are unstable in the stomach, systems that prolong delivery over the entire course of transits in the GI tract are beneficial; likewise, for systems that delay release until the dosage form reaches the small intestine. Compound that is unstable in the small intestine may demonstrate decreased bioavailability when administered from a sustaining dosage form. This is because more drugs is delivered in the small intestine and, hence, is subject to degradation.
Protein Binding
It is well known that many drugs bind to plasma proteins with concomitant influence on the duration of drug action. Since blood proteins are four the most part recirculated and not eliminated, drug protein binding can serve as the depot for drug producing a prolonged release profile, especially if high degree of drug binding occurs. There are, however, other drug – protein interaction that have bearing on drug performance.
CLASSIFICATION7, 8, 9, 10, 11, 12
The most common methods used to achieve sustained release of orally administered drugs are as follows:
Diffusion Systems
Diffusion systems are characterized by the release rate of drug being dependent on its diffusion through an inert membrane barrier. Usually, this barrier is an insoluble polymer. In general, two types or subclasses of diffusional systems are recognized reservoir devices and matrix devices.
a) Reservoir Devices
Reservoir devices, as the name implies, are characterized by a core of drug, the reservoir surrounded by a polymeric membrane. The nature of the membrane determines the rate of release of drug from the system. It is also possible to use polymer coatings to achieve sustained release. For this purpose the polymer itself should not dissolve, but rather should allow the drug to diffusion through the polymer membrane to the outside, in the case of oral drug delivery, into the gastrointestinal tract.
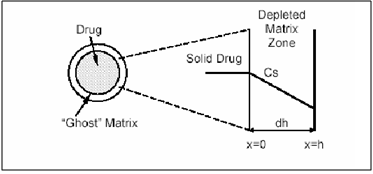
Figure 3. Schematic representation of a reservoir diffusional device.
b) Matrix Devices
A matrix device, as the name implies, consist of drug dispersed homogeneously throughout a polymer matrix. In the model, drug in the outside layer exposed to the bathing solution is dissolved first and then diffuses out of the matrix. This process continues with the interface between the bathing solution and the solid drug moving towards the interior, obviously, for this system to be diffusion controlled, the rate of dissolution of drug particles within the matrix must be much faster that the diffusion ate of dissolved drug leaving the matrix.
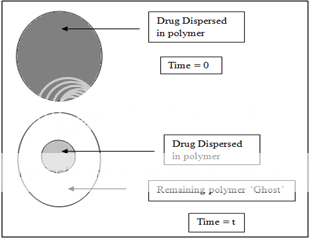
Figure 4. Matrix diffusional system before drug release (time=0) and after partial drug release (time=t).
Dissolution Systems
It seems inherently obvious that a drug with a slow dissolution rate will demonstrate sustaining properties, since the release of drug will be limited by the rate of dissolution. This being true, sustained-release preparation of drugs could be made by decreasing their rate of dissolution. The approaches to achieve this include preparing appropriate salts or derivatives, coating the drug with a slowly dissolving material, or incorporating it into a tablet with a slowly dissolving carrier.
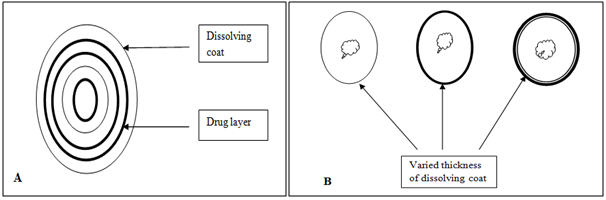
Figure 5. Two types of dissolution-controlled delivery system: (A) single bead type device with alternating drug and rate controlling layer; (B) beads containing drug with differing thickness of dissolving coats.
Osmotic System
Osmotic pressure is employed as the driving force to generate a constant release of drug. Consider semipermeable membrane that is permeable to water, but not to drug.When this device is exposed to water or any body fluid, Water will flow into the tablet owing to the osmotic pressure difference. These systems generally appear in two different forms. The first contains the drug as a solid core together with electrolyte, which is dissolved by the incoming water. The electrolyte provides the high osmotic pressure difference. The second system contains the drug in solution in an impermeable membrane within the device.

Figure 6. Diagrammatic representation of two types of osmotically controlled system.
Ion-Exchange Resins
Ion-exchange systems generally use resins composed of water-insoluble cross-linked polymers. These polymers contain salt-forming functional groups in repeating positions on the polymer chain. The drug is bound to the resin and released by exchanging with appropriately charged ions in contact with the ion-exchange groups.
Resin+ - drug - + X- resin+ - = X- + drug –
Conversely,
Resin- - drug+ + Y+ resin- - = Y+ + drug+
The free drug diffuses out of the resin. The drug-resin complex is prepared either by repeated exposure of the resin to the drug in a chromatography column, or by prolonged contact in solution.
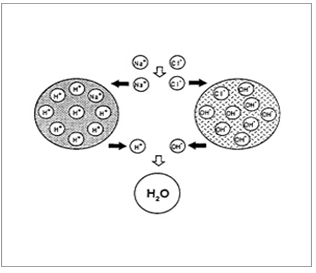
Figure 7. Diagrammatic representation of Ion Exchange resins.
Swelling and Expansion Systems
Conventional hydrogels swell slowly upon contact with water due to their small pore size, which usually ranges in the nanometers and low-micrometer scale. However if the hydrogel has a pore size of more than 100 µm, swelling is much faster and may lead to a large increase in size. Swelling ratios of over 100 can be achieved. These swollen systems become too large to pass through the pylorus and thus may be retained in the stomach even after housekeeper wave, provided they have a sufficiently high mechanical strength to withstand the peristaltic movement in the antrum of the stomach.
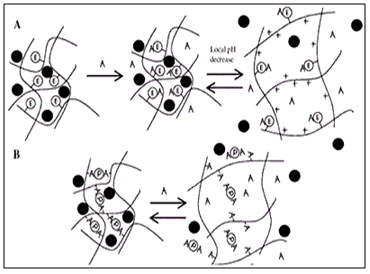
Figure 8. Diagrammatic representation of Swellingand Expansion Systems.
Floating Systems
If the dosage form has a lower density than the gastric fluids, it will float on a top of the stomach content, allowing for an increased time span to release the drug before the system is emptied out into small intestine. The gastric fluid has a density of approximately 1gm/cm3. If the density of the dosage form is lower than that, it will float on the gastric fluids. These systems require the presence of sufficient fluid in the stomach and the presence of food as discussed above. Several types of low density ingle-unit dosage forms (tablets) and multiple-unit dosage forms (pellets) have been developed. If a dosage form has density of larger than approximately 2.5gm/cm3, it will sink to the bottom of the stomach and pellets may be trapped in the folds of the gastric wall.
Bioadhesive or Mucoadhesive Systems
It has also been suggested to use Bioadhesive or Mucoadhesive polymers such as polyacrylic acid and chitosen to achieve gastric retention. The basic idea here is that the mucoadhesive or bioadhesive polymers leads to the dosage forms sticking on to the mucus of the gastric wall. Whilst the bioadhesive or mucoadhesive approach is a sensible one for buccal or sublingual formulations, due to rapid turnover of the mucus in the stomach, for gastroretentive systems this approach is not as straightforward. Finally magnetic materials may be added to the dosage forms. These systems can then be held in place by an external magnate, but this approach requires a precise positioning of the external magnate and is not likely to have a high patient compliance.
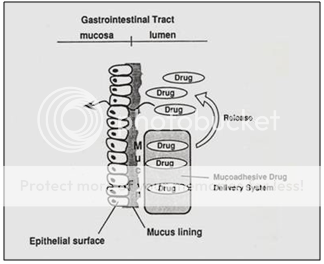
Figure 10. Diagrammatic representation of Bioadhesiveor Mucoadhesive systems.
Matrix Systems
One of the least complicated approaches to the manufacture of sustained release dosage forms involves the direct compression of blends of drug, retardant materials and additives to form a tablet in which drug is embedded in matrix core of the retardant. Alternately, retardant drug blends may be granulated prior to compression.
TYPES OF MATRIX
Hydrophobic Matrices
In this method of obtaining sustained release from an oral dosage form, drug is mixed with an inert or hydrophobic polymer and then compressed in to a tablet. Sustained release is produced due to the fact that the dissolving drug has diffused through a network of channels that exist between compacted polymer particles. Examples of materials that have been used as inert or hydrophobic matrices include polyethylene, polyvinyl chloride, ethyl cellulose and acrylate polymers and their copolymers.
Lipid Matrices
These matrices prepared by the lipid waxes and related materials. Drug release from such matrices occurs through both pore diffusion and erosion. Release characteristics are therefore more sensitive to digestive fluid composition than to totally insoluble polymer matrix. Carnauba wax in combination with stearyl alcohol or stearic acid has been utilized for retardant base for many sustained release formulation.
Hydrophilic Matrices
A matrix is defined as well mixed composite of one or more drugs with a gelling agent (hydrophilic polymer). These systems are called swellable controlled release systems. The polymers used in the preparation of hydrophilic matrices are divided in to three broad groups,
A. Cellulose derivatives:Methylcellulose 400 and 4000cPs, Hydroxyethylcellulose; Hydroxypropylmethylcellulose (HPMC) 25, 100, 4000 and 15000cPs; and Sodium carboxymethylcellulose.
B. Non cellulose natural or semi synthetic polymers:Agar-Agar; Carob gum; Alginates; Molasses; Polysaccharides of mannose and galactose, chitosan and modified starches.
Biodegradable Matrices
These consist of the polymers which comprised of monomers linked to one another through functional groups and have unstable linkage in the backbone. They are biologically degraded or eroded by enzymes generated by surrounding living cells or by nonenzymetic process in to oligomers and monomers that can be metabolized or excreted. Examples are natural polymers such as proteins and polysaccharides; modified natural polymers; synthetic polymers such as aliphatic poly (esters) and poly anhydrides.
Mineral Matrices
These consist of polymers which are obtained from various species of seaweeds. Example is Alginic acid which is a hydrophilic carbohydrate obtained from species of brown seaweeds (Phaephyceae) by the use of dilute alkali.
On the Basis of Porosity of Matrix: Matrix tablets can be divided in to 3 types.
· Macro porous Systems: In such systems the diffusion of drug occurs through pores of matrix, which are of size range 0.1 to 1 μm. This pore size is larger than diffusant molecule size.
· Micro porous System: Diffusion in this type of system occurs essentially through pores. For micro porous systems, pore size ranges between 50 – 200 A°, which is slightly larger than diffusant molecules size.
· Non-porous System: Non-porous systems have no pores and the molecules diffuse through the network meshes. In this case, only the polymeric phase exists and no pore phase is present.
MASRx AND COSRx SUSTAINED-RELEASE TECHNOLOGY13, 14, 15
MASRx Technology
The objective is to assess factors affecting drug release from guar-gum-based once-daily matrix sustained-release formulations (MASRx). The tablets were designed to hydrate completely into the tablet core. In the process, the tablet core expanded and released the drug in a sustained-release manner.
COSRx Technology
Formulations base on constant sustained-release matrix (COSRx) technology can also be developed using guar gum as a major rate-controlling polymeric material. Depending on the solubility of the drug, low- or high-viscosity guar gum can be use. The formulation involves a guar-gum-base tablet and a combination of water-soluble and water-insoluble polymeric tablet coat. When the tablet is placed in a dissolution medium, there is slow diffusion of water through the polymeric wall leading to swelling and gelations of the guar gum/drug core. As the hydration a progress, the tablet continues to swell until the wall breaks, forming a sandwich-like structure. The release of drug proceeds primarily out of the sides of the tablet as it passes through the intestinal tract. The tablets provide a nearly zero-order drug release following a programmed period of delayed drug release.
DRUG RELEASE MECHANISM FROM MATRIX SYSTEMS16, 17, 18
Zero Order Kinetics
A zero order release would be predicted by the following equation,
Qt - Q0 = K0t
Where, Qt = Amount of drug release dissolved in time‘t’.
Qo = Initial amount of drug concentration in solution.
K0t = Zero order rate constant.
When the data was plotted as cumulative % drug release verses time, if the plot is linear then data obeys zero order kinetics with slope equal to Ko. This model represents an ideal release profile in order to achieve the prolonged pharmacological action.
First Order Kinetics
A first order release would be predicted by the following equation
Log Qt = Log Qo - K1t/2.303
Where, Qt = Amount of drug released in time‘t’.
Qo = Initial amount of drug concentration in solution.
K1t = First order rate constant.
When data was plotted as log cumulative % drug remaining verses time yields a straight line indicating that the release follows first order kinetics. The constant K can be obtained multiplying slope values.
Higuchi’s Model
Drug release from the matrix device by diffusion has been described by Higuchi’s Diffusion equation
ft = Q = √Dδ/τ (2C- δCs)Cst
Where, Q = Amount of drug released in time‘t’.
D = Diffusion coefficient of the drug in the matrix.
Cs = Solubility of the drug in the matrix.
δ= Porosity of matrix.
τ= Tortuosity.
t = Time (h).
The equation may be simplified then equation becomes;
ft = Q = KH X t1/2
Where, KH = Higuchi dissolution constant.
When data was plotted according to this equation, i.e., cumulative drug released verses square root of time, yields a straight line, indicating that the drug was released by diffusion mechanism.
Peppas Korsmeyer Equation
In 1983 Korsmeyer et al. (Korsmeyer et al, 1983) developed a simple, semi-empiric model, when diffusion is the main drug release mechanism, relating exponentially the drug release to the elapsed time (t).
At/A∞= ktn
Where, k = Constant.
n = Release.
t = Time.
At and A∞= Absolutecumulative amount of drug released at time’t’.
This is used when the release mechanism is not well known or when more than one type of release phenomenon could be involved.
Hixon-Crowell Equation
Drug released from the matrix device by diffusion has been described by Hixon-Crowell diffusion equation;
W01/3 - Wt1/3 = ?t
Where, W0 = Initial amount of drug.
Wt = Remaining amount of drug.
t = Time.
? = Constant (Kappa).
This expression applies to pharmaceutical dosage form such as tablets where the dissolution occurs in planes that are parallel to drug surface if tablet dimensions diminish proportionally in such manner that the initial geometrical form keeps constant all the time.
PHARMACOKINETICS AND PHARMACODYNAMICS CONSIDERATION19
To achieve controlled drug delivery, it is desirable to have a zero-order drug input. Under steady state, rate in = rate out then
R0 = CssCL
This equation shows that the input rate of a controlled release is determined solely by steady state concentration and plasma clearance, t1/2, a common pharmacokinetic parameter is not directly needed to determine the input rate. However, it does play a role in determining the benefits of formulating a drug into controlled-release dosage form. Usually drugs of t1/2 more than 8 hours are not suitable candidates for controlled or sustained release dosage forms because they do not provide benefits over conventional dosage forms. In addition, t1/2 may be useful in determining the dosing interval of controlled release dosage forms. Similarly, volume of distribution is not major consideration in designing controlled-release delivery systems, although often a larger volume of distribution requires a higher drug load to achieve therapeutic blood level. However, there may not exist a direct correlation between pharmacokinetics and pharmacodynamics of a drug. In other words, it may be difficult to predict the effect of a drug based only on pharmacokinetics data. As a result, a PK/PD model required to obtained a rational design of a controlled-release dosage form. Typically a graded response can be represented by
E= PC + E0
Where, P is the proportionality constant, C is the plasma concentration, and E0 is the base line effect. In some cases, a more satisfactory relationship is obtained by using,
E = P log C + E0
In fact, in most cases, the relationship is much more complex than simple linear one, and sometimes it can be represented only by an expression closely related to enzyme kinetics,
E = E0 + (Emax Cn) / (En50) + Cn
CONCLUSION
By the above discussion, it can be easily conclude that development of sustained release dosage form which will prolong the drug release leading to minimize the peak and valley effect in plasma and provide patients compliance. The advantages of sustained release tablets or capsules are that they can often be taken less frequently than instant formulations of the same drug and that they keep steadier levels of the drug in the bloodstream. By several approaches the residences time of drug delivery system in the gastrointestinal tract can be prolonged. Difference between controlled release and sustained release is that controlled release is perfectly zero order release that is, the drug releases with time irrespective of concentration. On the other hand, sustained release implies slow release of the drug over time period. It may or may not be controlled release.
ACKNOWLEDGEMENT
We thank our management of K. T. Patil college of Pharmacy, Osmanabad for providing required support for completing this research work successfully.
REFERENCES
1. Jain KK. Drug delivery systems. 1st edition. Switzerland: Humana Press; 2008. P. 1-51.
2. Lachman L, Herbert AL, Joseph LK. The theory and practice of industrial pharmacy. 3rd edition. Bombay: Varghese publishing house; 1986. P. 430-455.
3. Joseph RR, Vincent HLL. Controlled drug delivery fundamentals and applications. 2nd edition revised and expanded. New York: Marcel Dekker Inc; 1987. P. 3-56.
4. Chien YW. Novel drug delivery system. 2nd edition revised and expanded. New York: Informa health care; 2009. P. 1-50.
5. Paul B, Gupta PK, Ara HD, John EH. Remington the science and practice of pharmacy. 21st edition. New York: Wolter kluwer, Lippincott wiliams and Wilkins; 2006. P. 939-962.
6. Edith M. Encyclopedia of controlled drug delivery. 1st edition. New York: A wiley interscience publication; 2009. P. 381-385.
7. Gilbert SB, Christopher TR. Modern pharmaceutics. 3rd edition revised and expanded. New York: Marcel Dekker Inc; 1995. P. 575-608.
8. Donald LW. Handbook of pharmaceutical controlled release technology. 1st edition. New York: Marcel Dekker Inc; 2000. P. 431-460.
9. Yvonne p, Thomas R. Pharmaceutics-Drug delivering targeting. 1st edition. Pharmaceutical press; 2010. P. 85-115, 117-139.
10. James S. Encyclopedia of pharmaceutical technology. 3rd edition. New York: Informa health care; 2007. P. 1082-1103.
11. Khan GM. Controlled release oral dosage forms: Some recent advances in matrix type drug delivery system: A Review article. Asian network for scientific information. 2001 Sept-Oct; 1(5); 350-354.
12. Patel H, Dhrupesh R, Patel PU, Suthar M. Matrix type drug delivery system: A Review. Journal of pharmaceutical science and bioscientific research. 2011 Nov-Dec; 1(3); 143-151.
13. Sakr AM, Elsabbagh HM. Correlation of water absorption with the disintegration effectiveness of guar gum. Pharm Ind. 1975; 37; 457-459.
14. Rudnick EM, Rhodes CR, Schwartz JB. Some effects of relatively low levels of eight tablet disintegration on direct compression system. Drug Dev Ind Pharm. 1981; 7; 347-358.
15. Altaf SA, Yu AL, Parasrampuria J, Friend DR. Guar gum based sustained release diltiazem. Pharm Res. 1998; 15; 1196-1201.
16. Paulo C, Lobo JMS. Modeling and comparison of dissolution profiles. European Journal of Pharmaceutical Sciences. 2001; 13; 123-133.
17. Kalam MA, Humayun M, Parvez N. Release kinetics of modified pharmaceutical dosage forms: A review. J. Pharmaceutical Sciences. 2007; 1; 30-35.
18. Dash S, Murthy P, Chowdhury P. Kinetic modeling on drug release from controlled drug delivery systems: A review. Acta Poloniae Pharmaceutica - Drug Research. 2010; 67(3); 217-223.
19. Paul B, Gupta PK, Ara HD, John EH. Remington the science and practice of pharmacy. 21st edition. New York: Wolter kluwer, Lippincott wiliams and Wilkins; 2006. P. 939-962.
NOW YOU CAN ALSO PUBLISH YOUR ARTICLE ONLINE.
SUBMIT YOUR ARTICLE/PROJECT AT articles@pharmatutor.org
Subscribe to PharmaTutor Alerts by Email
FIND OUT MORE ARTICLES AT OUR DATABASE









